太田さん(桑名若菜)が差し出す対戦カードをわたしが切り、滝沢くん (早稲田大)が切り、島原くん(東大阪)が切るという対戦前のバトルが繰り広げられた末、 結局わたしが不戦でした。(^o^)
2回戦は元クインの山崎みゆきさんとの対戦で敗れて早々に終わってしまい、 雑談モードに入っていると、伏見さん(奈良)いわく、 ランダムだったら不戦の期待値は3分の1になるということでした。 期待値が3分の1ということは、3回大会に出たら、そのうち1回くらいは不戦になるだろうということです。 寝つかれないときに計算したらしく、残念ながらどうやって導きだしたかはそのときはもう覚えていませんでした。
ほんまかなあと検証するためメモを取り出し、 わたしが今年にはいってから出場した7大会 (和歌山、高松宮杯、新春京都、奈良、大阪、東大阪、桑名) のA級の出場人数と1回戦不戦人数ののべ数で計算してみると、
期待値=不戦人数/出場人数=104 / 344 = 0.302
と、なかなかいい線いっています。
後日、どうやったら1/3という数字がでてくるか検討してみました。
X … 出場人数
Y … 不戦人数
α … 2^α ≦ X < 2^(α+1) となる整数
n … 出場人数のうち2^α からはみだしている人数
例)出場人数36名の場合、次のようになります。
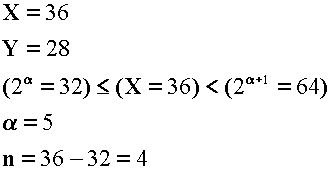
出場人数X および はみだし人数nは次式で示されます。
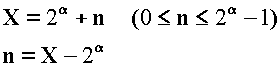
不戦人数Yは、出場者数からはみだし人数を減らすための対戦者数を引くことで得られますので、次式で示されます。
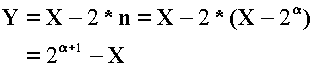
この式より、不戦人数Yは、Xが大きくなるにしたがって右下がりののこぎり歯がだんだん大きくなっていくグラフになることがわかります。
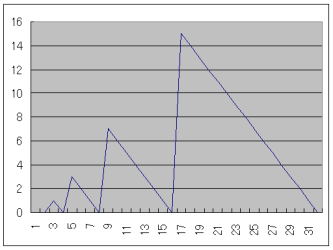
1つの大会で不戦となる期待値Eは次式で与えられます。
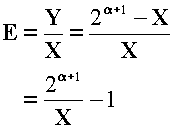
ここで、Xが一様に分布すると仮定すると、それぞれののこぎりの歯の中心が全体としてみた期待値になります。
のこぎりの歯の中心Xcは
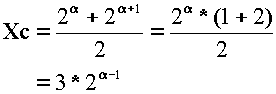
したがって、全体としてみた不戦の期待値は
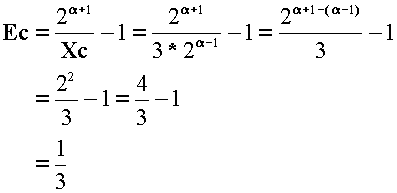
どののこぎりの歯に関わらず1/3となります。
実際の大会においては、はみだし人数がごく少数名の場合に回戦数を減らす目的で、大会を運営している会の選手が出場辞退して調整することも多いため、期待値は1/3よりやや小さくなるでしょう。