
(to Mathematics top ->)
何故a^0=1?
そうですね。一言で言えば、「そう決めるのが都合が良いし、自然だから」です。
なぜでしょうか。
累乗指数a^bを導入したのはデカルト、bを有理数及び負の数まで定義したのはウォリスと言われています。
わかりやすくa=10で考えてみましょう。
bが自然数(1,2,3,…)のときは問題ないですね。
10^1=10、10^2=10×10、10^3=10×10×10、… です。このとき自然数m,nに対して明らかに次の式が成り立ちます。
10^m×10^n=10^(m+n) (1)
(∵ (10×10×10×…(m個))×(10×10×10×…(n個))で、括弧を払えばよい)
逆を考えてみれば、m>nならば次式も明らかです。
10^m÷10^n=10^(m-n) (2)
また、次の式も明らかでしょう。
(10^m)^n=10^(m×n) (3)
(∵ (10^m)^n=(10^m×10^m×…(n個))=10^(m+m+…(n個))=10^(m×n) …(1)より)
さて、ここまでは「a^bはaをb回掛けたものである」という普通の素朴な定義からわかる話です。
ここからはウォリスがやったように定義を拡張してみましょう。
まず、10^bで、bが分数のときはどうでしょうか。
例えば10^(1/2)を考えてみましょう。
「1/2乗」というものを新たに定義するわけですが、あくまで「累乗」として定義するわけですから、整数乗と同じ性質を持つように定義するのが「自然」でしょう。
つまり、(1)〜(3)式が成り立つように定義するべきです注1)。
すると、(1)式より 10^(1/2)×10^(1/2)=10^1=10 になるべきですから、10^(1/2)=√10 です。
この定義が(2),(3)式も満たせることを確かめてください。
同様に10^(n/m)も定義できる事がわかると思います。
さらに、10^(√2)=10^1.4142… のような無理数乗も、同様に定義できるだろうことはお分かりでしょう注2)。
次に、10^bでbが0や負の場合はというと、(2)からまず整数ならば 10^1÷10^2=10^(-1) となるはずですが、10^1÷10^2は1/10ですから、10^(-1)は1/10と定義すべきでしょう。
さらにいろいろな場合を考えてみれば、 10^(-b)=1/10^b と定義すると全てうまくいくことが分かります。
10^0も同様で、10^2÷10^2=10^(2-2) 等を考えれば1でなければならないことが理解されると思います。
これで10^xのxに整数以外の実数も「自然に」入れられるようになりました(しつこく繰り返しますが、「自然に」とは最初の累乗の性質である(1)〜(3)式を満たすようにということです)。
そんなわけでy=10^xのグラフを下のように描くことが出来るようになったわけです。
グラフが滑らかな曲線になっているのが、自然に拡張された証拠ともいえます。
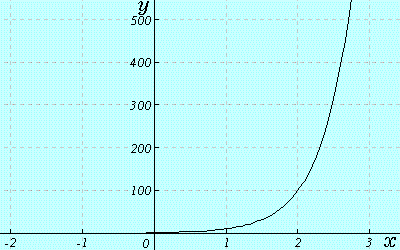
図1.y=10^xのグラフ
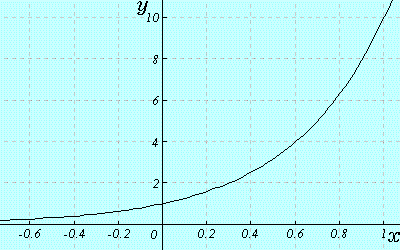
図2.y=10^xのグラフ(原点付近拡大)
これで本当に便利になりましたね。
え?単に適当に定義を拡張しただけで、何が便利かわからないって?
(1)〜(3)をもう一度良く見てください。
これらの式が示していることは、10^bの形の数ならば、掛け算が足し算で計算出来て(式(1))、割り算が引き算で計算出来て(式(2))、累乗が掛け算で計算出来る(式(3))ということです。
要するに、10^bの形の数ならば、計算が楽になるということです。
そして、上で長々と説明してきたことはグラフでも分かるように、全ての正の数は10^bの形で表されるということです。
つまり、もうおわかりでしょうが、累乗指数の定義の拡張はもともと計算を楽にするために行なわれたもので、 a^0=1 というのもその一環なわけです。
例えば掛け算A×Bをこの方法で計算するには次のようにします。
(1-1)A=10^aになるようなaを求める。
(1-2)B=10^bになるようなbを求める。
(2)c=a+bを求める。
(3)10^c=CになるようなCを求める。CがA×Bの答。
(1)と(3)では前もって作ってあった表(y=10^xのyとxの関係を表にしたもの)を使えば良いわけです。
いちいち「A=10^aになるようなa」などと言うのはやっかいなので、 a=logA で表して、aをAの「対数」といいます注3)。
この対数が、計算機がなかった時代に複雑な計算のためにどんなに役立ったかは言うまでもないでしょう注4)。
注1)
(1)〜(3)式が成り立つように定義するべき
そういう風に定義しないと、拡張の意味がありません。このようになるべくそれまでの法則が成り立つように拡張することを「算法不易の法則」と言ったりします。a^bはこのように自然に拡張されますが、そうでない場合もあります。少し不自然にしか拡張できない場合もありますし、自然な拡張法がいくつもある場合があります。こういう場合は「慣例」に従うとか、「これこれこういう定義を採った」と断るとかしなければいけません。
注2)
無理数乗も、同様に定義できる
細かいことを言い出すときりがありませんが、まあ感覚的には分かるでしょう。
注3)
このあたりはわざとだらだらとしつこく書いています。というのも、「対数なら知ってるよ、高校で習った」等と言いながら「a^0=1がわからない」などと言う人が多いからです。対数が分かっていれば、a^0=1 は当然のこととして捉えているはずなのですが…。学校教育が悪いのでしょうかね(笑)。
注4)
対数が、計算機がなかった時代に…
現在では歴史的意味しかないのかもしれませんが、対数を感覚的につかむためにも、対数表ぐらいは使えるべきでしょう(まあ、対数を理解していれば対数表なんか使い方を習わなくても使えるはずですが)。僕は中学校のとき丸善の七桁対数表を買ってわくわくしながら眺めたものですが、今はそういう人も少ないのでしょうね。あと、対数の計算を使う道具の傑作といえば計算尺ですが、最近どこにも見かけなくなってしまいました。残念ですね。


