
(to Mathematics top ->)
e^πとπ^eはどっちが大きい?
良くある問題ですが、答だけなら実際に計算すればすぐ分かります。
e^π=23.14069…
π^e=22.45915…
なので、答は「e^πの方が大きい」です。もちろん、そんな話ではないですね。良くある問題は、それを簡単に(エレガントに)証明する方法でしょう。個人的に好きなのは次の証明方法です。
まず、y=x^(1/x)という関数を考えます。これがどんなグラフになるかを考えてみます。増減を調べるために微分してみると、x^(1/x)=exp{(1/x)log(x)}より、
{x^(1/x)}'=x^(1/x)・(1-log(x))/(x^2)
y'=0 とおくと x=e
lim[x→∞]{x^(1/x)}=1
lim[x→+0]{x^(1/x)}=0
に注意すると、次のような増減表が得られます。
y=x^(1/x)の増減表
| x |
(+0) |
|
e |
|
(∞) |
| y' |
|
+ |
0 |
- |
|
| y |
(0) |
増加 |
e^(1/e) |
減少 |
1 |
というわけで、グラフはこうなります。
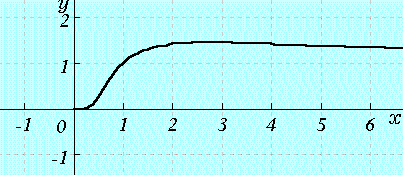
従って、y=x^(1/x)はx=eのときに最大値e^(1/e)を取ります。そこで、
e^(1/e)>π^(1/π)
両辺をeπ乗して
e^π>π^e
というわけです。

