
(to Mathematics top ->)
k人の人の中に同じ誕生日の人がいる確率
ある有名な数学者(ワーレン・ウィーバー?)が、あるとき22人の高級将校の夕食会に参加して、この確率について説明しました。そして会食者一人一人に誕生日を聞いたのですが、最後の一人まで聞いても同じ日に生まれた人はおらず、面目を失いかけました。ところが突然、その部屋にいた24人目の人が名乗りをあげました。それはたまたまそこにいたウエートレスで、彼女は出席していた将校と同じ日に生まれていたのです…。
という有名な(しかしちょっと出来過ぎた)話がある、有名な問題です。
この問題が有名なのは、感覚的な予想よりもずっとこの確率が高いからで、確率の話になると必ず出てきます。
さて、この、誕生日の同じ人が少なくとも一組いる確率は、23人で50%を越え、45人では約94%になります。このことを確かめてみましょう。
まず誕生日が同じにならない確率を求めます注1)。計算を簡単にするために、うるう年は考えないことにしましょう。二人の場合、片方の誕生日以外の日がもう一人の誕生日であれば良いので、確率は1-1/365=364/365。3人ならば、3人目がさらに別の誕生日なら良いわけですから、(1-1/365)×(1-2/365)=364×363/365^2。以下同様にしてk人ならば、
(1-1/365)×(1-2/365)×…×(1-(k-1)/365)=364×363×…×(365-(k-1))/365^(k-1)
というわけです。この値を1から引けば、誕生日の同じ人が少なくとも一組いる確率が求められます。
簡単な計算方法
まあ、電卓や表計算ソフトでやれば簡単ですが(笑)、せっかくですからちょっと工夫してみましょう。
というわけで次の近似式を使います。
1-r/n≒e^(-r/n) …(1)
1-r/n≒e^(-r/n-(r/n)^2/2) …(2)
…
この近似式はlog(1+x)=x-(x^2)/2+(x^3)/3-…という級数展開の最初の方の項を取ったものです。注2)
これから、k人の人の誕生日が全て異なる確率をp(k)とおくと、
p(k)≒e^(-(1+2+…+(k-1))/n)=e^(-k(k-1)/2n) …(1)より
p(k)≒e^(-(1+2+…+(k-1))/n-(1^2+2^2+…+(k-1)^2)/2n^2)
=e^(-k(k-1)/(2n)-k(k-1)(2k-1)/(12n^2)) …(2)より
(当然n=365です)
で、同じ誕生日の生徒が少なくとも一組いる確率1-p(k)をいろいろなkの値で計算してみると下表のようになります。
| k |
1-p(k) |
近似式(1) |
近似式(2) |
| 5 |
0.027136 |
0.027025 |
0.027135 |
| 10 |
0.116948 |
0.115991 |
0.116936 |
| 15 |
0.252901 |
0.249992 |
0.252843 |
| 20 |
0.411438 |
0.405805 |
0.411288 |
| 22 |
0.475695 |
0.468938 |
0.475496 |
| 23 |
0.507297 |
0.500002 |
0.507073 |
| 25 |
0.568700 |
0.560412 |
0.568422 |
| 30 |
0.706316 |
0.696320 |
0.705916 |
| 35 |
0.814383 |
0.804097 |
0.813905 |
| 40 |
0.891232 |
0.881990 |
0.890745 |
| 45 |
0.940976 |
0.933618 |
0.940546 |
| 50 |
0.970374 |
0.965131 |
0.970040 |
| 55 |
0.986262 |
0.982897 |
0.986032 |
| 60 |
0.994123 |
0.992166 |
0.993981 |
グラフも描いてみました。
これは近似式(2)によるものです。
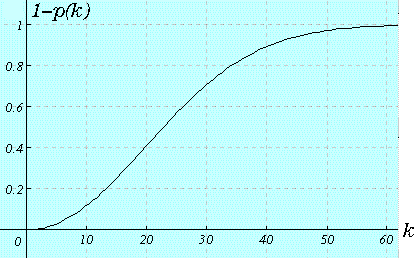
予想外に大きな値ですね。
確率には計算結果と感覚とが合わないことが良くありますが、これもその一例でしょう。
注1)
まず誕生日が同じにならない確率を求めます
何かが起こる確率を求めるために、起こらない確率を1から引く、というのは良くある手段です。この場合も、起こる確率を求めようとすると極めて面倒になってしまいます。
注2)
この近似式
(1)の近似式あるいは(1-a/n)^n≒e^(-a)はこの手の計算によく使われるので覚えておきましょう。例えば、1年間に起こる確率が1/10000の事象は10000年ならどれぐらいの確率で起こるか、とか。すぐに答えられますよね。

