競技かるたの最高クラス(4段以上)のA級選手の実力ランクについて調べるため、統計分析を行いました。この統計分析のために、A級公式個人トーナメント戦63大会2850試合(1996/07/28高校選手権個人戦〜1998/01/18東京東会大会)、出場A級選手数381名を対象に、トーナメント戦の勝抜き度(式2.1)を選手の実力を示す指標として用いています。
式2.1 勝抜き度Ktの定義
Kt=勝ち数/(出場大会数+1)
勝抜き度Ktはトーナメント戦における勝ち数の期待度を示しています。トーナメント戦では一度負けるとその段階で終わりなので、どれくらい勝ち数が期待できるかで実力を測ることができます。この分析の結果、A級選手の勝抜き度と実力ランクの関係は図2.1のように示されることがわかりました。
図2.1 A級選手における勝抜き度Ktと実力ランクとの対応
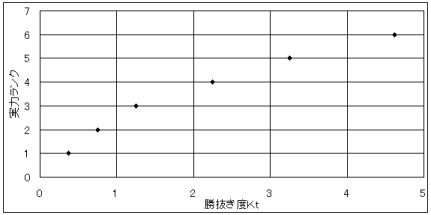
図2.2 競技かるたレーティング曲線
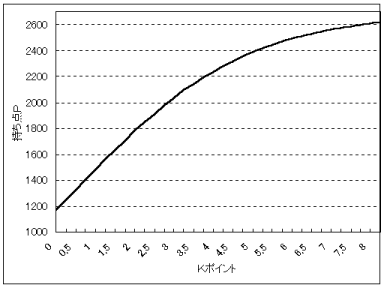
この勝抜き度と実力ランクの関係を表す近似曲線式を導いて、レーティングシステムの最も基礎となるレーティング曲線式とし、勝抜き度と実力ランクに対応する持ち点を関係づけました。関係づけにあたっては、将来A級選手から有段者全体まで対象にできるように、勝抜き度を式2.2で修正したKポイントを定めました。また小林好真さんの競技かるたレーティング(将棋レーティングをもとにした方法)や将棋やチェスのレーティングの持ち点の値と対比しやすいように、実力ランクを式2.3で対応づけた持ち点を定めました。
式2.2 Kポイントと勝抜き度Ktの対応式
Kポイント=Kt+3
式2.3 持ち点Pと実力ランクの対応式
持ち点P=2000+100*ランク
近似曲線式としては、最高ランクにおいては図2.1のカーブを満たし、それより下位ランクは直線的となる、ロジスティック曲線式をあてはめました。この曲線式がKポイントと持ち点Pの関係に最も適合するようにαβγを最小2乗法で探すと、γは式の単純化のために整数とすれば、式2.4が得られます。この式が競技かるたレーティングシステムの最も基礎となる式で、これを図示すると図2.2になります。
式2.4 競技かるたレーティング曲線式
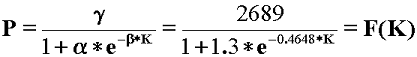
選手の持つ持ち点Pは曲線式で得られた曲線値の小数部を切り捨てた整数部です。各ランクにおける持ち点の理論値と実用値の対応を表2に示します。
表2 持ち点の理論値と実用値の対応
| 理論値 | 実用値 | |||||
|---|---|---|---|---|---|---|
| Kt | Kポイント | ランク | 持ち点 | 曲線値 | 持ち点 | 理論値との誤差 |
| 0.37 | 3.37 | 1 | 2100 | 2114.92 | 2114 | +14(+0.67%) |
| 0.75 | 3.75 | 2 | 2200 | 2190.64 | 2190 | -10(-0.45%) |
| 1.25 | 4.25 | 3 | 2300 | 2278.20 | 2278 | -22(-0.96%) |
| 2.25 | 5.25 | 4 | 2400 | 2415.37 | 2415 | +15(+0.63%) |
| 3.25 | 6.25 | 5 | 2500 | 2510.33 | 2510 | +10(+0.40%) |
| 4.62 | 7.62 | 6 | 2600 | 2591.43 | 2591 | -9(-0.35%) |
持ち点の実力目安をあげると、おおよそ、現在(1999年1月)の西郷直樹名人・渡辺令恵クインレベルは2500点、A級優勝レベルは2300点、A級昇級レベルは2000点です。現在のレーティング対象はA級のみのため下位の級の点数目安はありませんが、推定でB級昇級レベルは1800点、C級昇級レベルは1600点ぐらいだろうと考えます。
この競技かるたレーティング曲線の特徴は、少ない大会数で実力ランクが判断できる勝抜き度をレーティングの持ち点と対応づけていることです。勝抜き度はごく短期のうちは大会の勝ち数期待値を示しますが、長期的には大会の平均勝ち数と同等になって変化への対応力が非常に弱くなります。一方、レーティングによる持ち点変化はその時々の対戦結果によって実力ランクの変化を機敏に示しますが、持ち点初期値をどうやって定めるかという課題がつきまといます。
この勝抜き度とレーティングのお互いの特徴の利点を対応づけし、勝抜き度によって少ない大会数で高い精度の持ち点初期値を(人為的な手段や主観を介することなく)得て、そしてレーティングに継ぎ目なく入っていけるのが、この競技かるたレーティング曲線です。