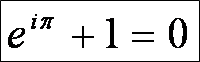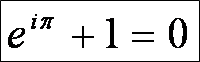
なんだろうと思って調べると、オイラーの公式でθ=πにしたら このオイラーの等式(かのノーベル賞物理学者ファインマンさんが 宝石と呼んだらしい)になるのがわかって、ふと競技かるたに重なる なあと思いました。
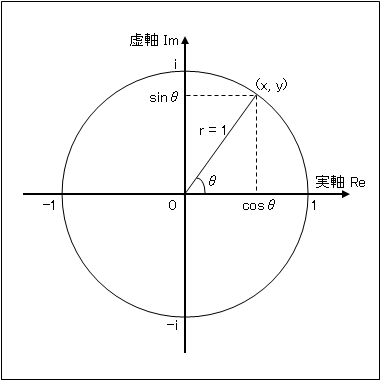
下記のオイラーの公式で左辺は極座標(長さr=1,角度θ)、 右辺は直交座標(実軸x=cosθ,虚軸y=sinθ)というふうな 座標の変換式ともいえます。
オイラーの公式
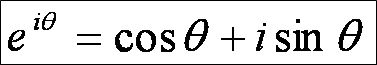
オイラーの公式の幾何学的表現
競技かるたをするとき、次のような流れで暗記する人も多いことと思います。
①各段ごとに札の並びを覚える。
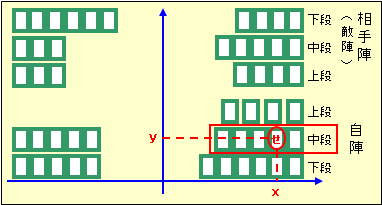
図1で「せ」の札は自陣中段(y軸)の右側の外から2枚目(x軸)にあるというように、 直交座標的に覚えている。
図1.各段の札の暗記(直交座標的な暗記)
②出だしの音が同じ札の位置関係を覚える。
「むすめふさほせ…」(一度覚えたら場にある札だけ)と順に言いながら 暗記もれの札がないようにして、出だしの音が同じ札の位置関係を図形で覚える。
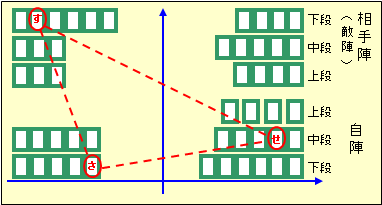
図2で「す」「さ」「せ」のS音で始まる札の位置関係を図形で覚えるとともに、 どのように取るか作戦を考える。
図2.出だしの音が同じ札の暗記(幾何学的な暗記)
③置いた手からの直線的位置関係で各札の位置を覚える。
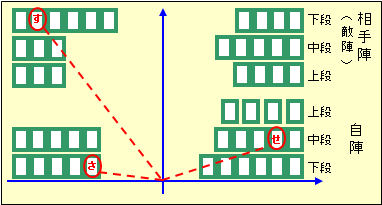
各札に対して直線的に行くのが基本的に最も早いため、置いた手から扇形を イメージして各札の位置を覚える。
図3.各札の暗記(極座標的な暗記)
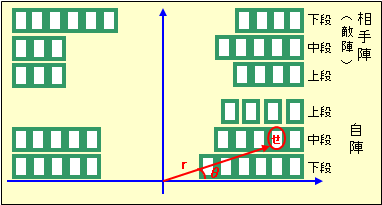
そして基本的には扇形をイメージして直線的に札を取りに行きます。
図4.出札を取る(極座標的な取り)
見事に直交座標から極座標に座標変換をしてますね。
そうやって座標変換して札を1枚1枚減らしていって、最後は枚数を 0にするゲームが競技かるたともいえるでしょう。
また競技かるたは相手(Enemy)と自分(I)とランダムに札を読む読手がいて ゲームができます。審判が原則いないため、相手と自分とでどちらが札を とったかを決めます。
e: 相手。(形が払い手をしているようにも見える)
i: 自分。(形が札に手を伸ばしているようにも見える)
π: 読手。(πと乱数は関係が深い。形が読手の使う読み台にも見える)
eがiより大きな文字: かるた道の精神が表現されているように感じる。
そう思ってあらためてこのオイラーの等式を見ると、宝石とも呼ばれる この数式が競技かるたを表現しているように見えてきます。
オイラーの等式